Limits are one of the first big ideas you’ll encounter in calculus—and they can feel a bit abstract at first. Why focus on what happens as a value approaches a number, rather than just plugging it in? Because limits unlock two of calculus’s most powerful tools: instantaneous change and continuity. Without them, much of modern mathematics would fall apart.

🔍 What Is a Limit?

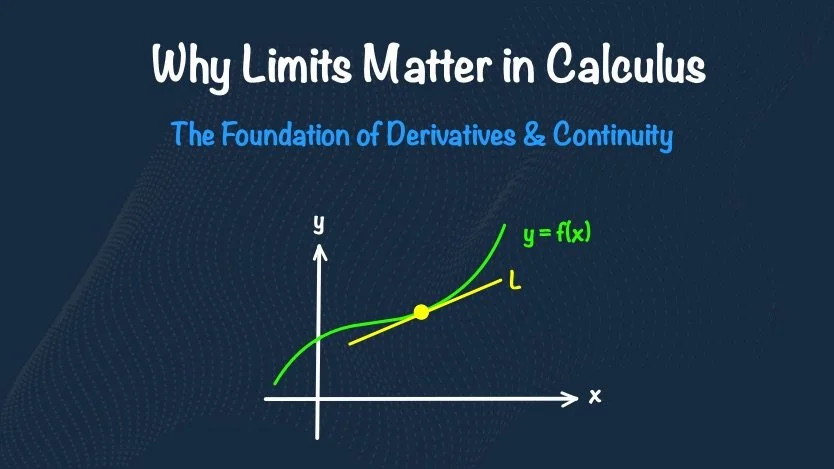
A limit describes the value a function approaches as the input (x-value) gets closer to a specific number. Think of it like zooming in on your GPS trail during a hike—not just to see where you are, but to understand the direction you're heading. Even if your current location is temporarily unclear (like a hole in a function), the GPS still shows your path and trajectory. Similarly, limits help us understand a function’s behavior near a point, even when direct substitution doesn’t work.

Take this example:

f(x)=(x^2−4)/(x-2)

If you plug in x=2, you get 0/0, which is an indeterminate form. But as you get infinitely close to x=2, the function approaches a specific value: 4. That’s the power of limits—they reveal behavior that isn’t obvious at first glance.

📈 Why Limits Are Essential in Calculus

Limits are the foundation of derivatives, which describe how things change at a single instant. The derivative tells us the slope of a curve at a precise point—something that seems impossible without limits.

• Velocity Example: A car’s average velocity is easy to calculate: distance divided by time. But if you want to know the exact speed at 1:05 PM, you need a derivative. And to define a derivative, you need limits.

• Continuity Example: Limits also help us understand continuity. A function is continuous if it flows smoothly—no gaps, jumps, or holes.

In physical systems like water flowing through a pipe or a rocket’s flight path, we expect smooth transitions. A discontinuous model might suggest the rocket suddenly jumps from one point to another—an unrealistic scenario in physics. Limits ensure our mathematical models behave like the real world.

🌍 Real-World Applications of Limits

Limits aren’t just theoretical—they’re woven into the fabric of real-world problem-solving across many disciplines.

• Engineering: Limits help analyze how stress behaves as a load approaches a material’s breaking point. This insight allows engineers to design structures that are both safe and efficient.

• Medicine: Limits are used to model how drug concentrations change over time. By understanding how levels approach a steady state or decline, researchers can predict a drug’s effectiveness and optimize dosage schedules.

• Economics: Limits play a key role in calculating marginal cost and marginal revenue—the change in cost or revenue from producing one additional unit. These instantaneous rates of change are essential for making smart business decisions.

In each of these fields, limits allow us to zoom in on critical moments, revealing behavior that average values alone would miss.

🎓 Why Students Should Care

If you’re preparing for calculus or just starting out, mastering limits will make everything else—derivatives, integrals, and real-world applications—much clearer.

Think of limits as the microscope of mathematics. They let you zoom in and see exactly what’s happening at a single instant. Without them, we’d be stuck with rough averages instead of precise answers.

So here’s a challenge: What everyday situations can you think of where an instantaneous change or smooth transition matters? A heart rate spike? A sudden stock price drop? That’s limits in action.

📚 Learn More with My Calculus Series

If this post sparked your curiosity about limits, my full Calculus 1 video series is designed to guide you through the next steps. On my YouTube channel, Understand the Math, I explain limits, derivatives, continuity, and more—step by step, with free guided notes to follow along.

Start exploring with the Calculus 1 Playlist and build a strong foundation in calculus concepts that you’ll use again and again in math, science, and engineering.