Introduction

Once you learn basic differentiation rules in Calculus 1, you quickly discover that not every function can be handled with just the power rule. That’s where the Product Rule, Quotient Rule, and Chain Rule come in.

These rules let us differentiate products, quotients, and compositions of functions, and they appear on nearly every exam.
In this guide, you’ll learn what each rule says, why it works, and how to apply it correctly with step-by-step examples (aligned with my Calculus 1 videos on Understand the Math).

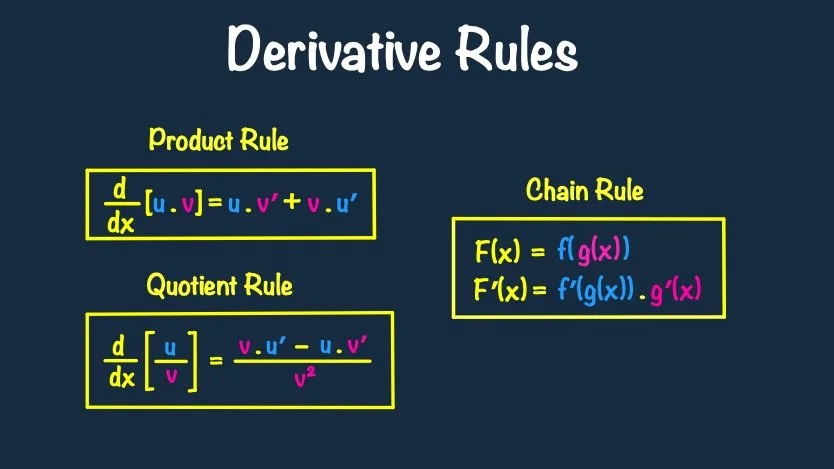
1. The Product Rule

The Product Rule is used to find the derivative of a function that is the product of two functions.

Formula
(fg)′ = f′(x) g(x) + f(x) g′(x)

In words: the derivative of a product is not the product of the derivatives — you multiply and add.
Mnemonic: “First times derivative of the second, plus the second times derivative of the first.”

Example 1
Find d/dx [x² eˣ]

f(x) = x²  f′(x) = 2x
g(x) = eˣ  g′(x) = eˣ

d/dx [x² eˣ] = (2x)eˣ + x²(eˣ) = eˣ(x² + 2x)

Example 2
Find d/dx [(3x² − 5)(x³ + 1)]

f(x) = 3x² − 5  f′(x) = 6x
g(x) = x³ + 1  g′(x) = 3x²

d/dx [(3x² − 5)(x³ + 1)] = (6x)(x³ + 1) + (3x² − 5)(3x²)

Simplify: 6x⁴ + 6x + 9x⁴ − 15x² = 15x⁴ − 15x² + 6x

2. The Quotient Rule

The Quotient Rule is used to find the derivative of a function that is the quotient of two functions.

Formula
(f / g)′ = [f′(x) g(x) − f(x) g′(x)] / [g(x)]²

Memory trick: “Low D High minus High D Low, all over the square of what’s below.”

Example 1
Find d/dx [(x² + 1) / (x³ − 2)]

f = x² + 1  f′ = 2x
g = x³ − 2  g′ = 3x²

d/dx [(x² + 1) / (x³ − 2)] = [(2x)(x³ − 2) − (x² + 1)(3x²)] / (x³ − 2)²

Example 2
Find d/dx [sin x / x]

f = sin x  f′ = cos x
g = x    g′ = 1

d/dx [sin x / x] = [x cos x − sin x] / x²

3. The Chain Rule

The Chain Rule is used to find the derivative of a composite function.

Formula (Function Composition)
y = f(g(x)) ⟹ dy/dx = f′(g(x)) · g′(x)

Formula (Leibniz Notation)
If u = g(x), then dy/dx = (dy/du) · (du/dx)

In words: take the derivative of the outer function (keep the inside the same), then multiply by the derivative of the inner.

Example 1
Find d/dx [(3x² + 1)⁵]

Outer f(u) = u⁵ ⇒ f′(u) = 5u⁴
Inner g(x) = 3x² + 1 ⇒ g′(x) = 6x

dy/dx = 5(3x² + 1)⁴ · 6x = 30x(3x² + 1)⁴

Example 2
Find d/dx [sin(x³)]

Outer f(u) = sin u ⇒ f′(u) = cos u
Inner g(x) = x³  ⇒ g′(x) = 3x²

d/dx [sin(x³)] = cos(x³) · 3x² = 3x² cos(x³)

Example 3
Find d/dx [e^(5x² + 4x)]

Outer f(u) = eᵘ ⇒ f′(u) = eᵘ
Inner g(x) = 5x² + 4x ⇒ g′(x) = 10x + 4

d/dx [e^(5x² + 4x)] = e^(5x² + 4x) (10x + 4)

Example 4
Find d/dx [ln(3x² + 7)]

Outer f(u) = ln u ⇒ f′(u) = 1 / u
Inner g(x) = 3x² + 7 ⇒ g′(x) = 6x

d/dx [ln(3x² + 7)] = (1 / (3x² + 7)) · 6x = 6x / (3x² + 7)

4. Combining the Rules

Many real problems require more than one rule at a time.
When you see parentheses, fractions, and products together, slow down and identify layers.

Example
Find d/dx [(x² sin(3x)) / eˣ]

Step 1. Identify each part
Numerator = x² sin(3x)
Denominator = eˣ

This problem needs all three differentiation rules:
• Quotient Rule for the overall fraction
• Product Rule for x² sin(3x)
• Chain Rule for sin(3x)

Step 2. Differentiate the numerator
Let u = x² sin(3x)

u′ = (2x) sin(3x) + x² (3 cos(3x))
= 2x sin(3x) + 3x² cos(3x)

Step 3. Differentiate the denominator
v = eˣ ⟹ v′ = eˣ

Step 4. Apply the Quotient Rule
Derivative = (u′v − u v′) / v²

Substitute each piece:
[(2x sin(3x) + 3x² cos(3x)) eˣ − (x² sin(3x)) eˣ] / (eˣ)²

Simplify by canceling one eˣ:
[(2x sin(3x) + 3x² cos(3x) − x² sin(3x))] / eˣ

Step 5. Combine like terms
[(2x − x²) sin(3x) + 3x² cos(3x)] / eˣ

That’s the final simplified answer.

5. Key Takeaways

Product Rule  (fg)′ = f′g + fg′
Quotient Rule  (f/g)′ = (f′g − fg′) / g²
Chain Rule  (f(g(x)))′ = f′(g(x)) g′(x)

Always identify the structure first; simplify only after differentiating.

Conclusion

The Product, Quotient, and Chain Rules are at the heart of differentiation in Calculus 1. They allow us to take derivatives of functions built from other functions — and they open the door to applications in physics, engineering, and economics.

Want to see every rule demonstrated step-by-step?

Watch the Product and Quotient Rule and Chain Rule videos on YouTube and download the guided notes: